Camera Calibration on a curved surface

[swanprince]

Hello,

I am trying to use OpenCV’s camera calibration to “flatten” images on a concave surface. The camera is statically positioned facing the center of the surface throughout my experiments, so I think I can get away with taking sample photos from the same position. I have gone through the Camera Calibration tutorial, which works well enough when the pattern is on a flat surface, but on a curved surface the top and bottom edges curve inwards even when corrected. I originally used the circle grid pattern, but because that doesn’t really capture the curvature as well as I’d like I switched to a grid of lines, then found their intersections with each other and the screen borders to use as my image points. See below for an example:

I can find the points well enough, but when I run these points through cv.calibrateCamera and correct the image using the functions outlined in the tutorial, it doesn’t seem to actually correct the image. There are still very clear curves at the top and bottom.

Is what I’m doing the correct approach to undo the curvature in the images? Or do I need to use a custom re-mapping function or something else? What am I doing wrong here?

Thank you!

[Steve_in_Denver]

If I’m understanding your setup correctly, I think you might need something more than the camera calibration and related functions.

Camera calibration is about modeling the mapping from 3D (world) to 2D (image), and has been developed to work for typical cameras and lenses. The model consists of the theoretical pinhole model (image center, focal length) and a distortion model to account for distortions due to physical factors (sensor tilt, lens distortion). The lens distortion part is your only hope, but it’s probably not a good fit.

The distortions you get from the concave surface aren’t necessarily something the camera calibration functions can model. For example, the distortion model is based on an assumption that the distortion is radially symmetric about the image center, so a distortion that behaves differently in the X axis vs the Y won’t be modelled correctly.

I’m not sure how I’d approach this - it would depend on other factors and exactly what you are trying to do.

Can you describe the “image on a cylinder” part a little better? Is it light being projected onto a screen for viewing? What is the end goal? To be able to process the camera image so it appears rectangular as if the cylinder were unrolled?

[swanprince]

@Steve_in_Denver

Can you describe the “image on a cylinder” part a little better? Is it light being projected onto a screen for viewing?

Let’s say it’s a bent piece of paper for now.

@Steve_in_Denver

What is the end goal? To be able to process the camera image so it appears rectangular as if the cylinder were unrolled?

Yes, that’s the end goal.

At the moment, I am considering calibrating the camera on a flat surface first, then determining the perspective matrix (or equivalent) using the concave surface. I don’t know if a OpenCV perspective transform functions will handle curves very well, though, so I may need to use some other mapping function if that doesn’t work.

[crackwitz]

optical flow and remap()

• prepare a target pattern (digital original)
  • it should cover the entire view and be decently dense.
  • yours looks dense enough, but it doesn’t yet cover the whole view.
• start with a map for remap(). it will pull from the distorted image into “pattern” space.
• loop until nice:
  • smooth the map (gaussian, stackblur, …)
    • the boundary can “pull” on the map, round it off there. a cross section of the map, to the smoothing algorithm (borderMode nearest?), looks like an escalator (flat low, rising, flat high) and the smoothing will round those obtuse angles off, introducing distortion. I think that could be worked around but I didn’t bother with that so far.
  • remap(), with the map, from the distorted image, to a temporary image
  • calculate optical flow temp ↔ target (in some suitable direction), obtain error map
  • add error to map
    • by remapping the map, using the error map. that should converge quickest.
    • simply summing the maps elementwise seems to do well enough

that description probably contains undefinitions/errors of direction/sign in various places. fiddle with it, prototype on manually generated distortion maps that give you synthetic distortion.

I think I once implemented this here: https://stackoverflow.com/questions/76092964/remove-pincushion-lens-distortion-in-python/76176980#76176980 and I have the complete code somewhere too, if required. the inline snippets in the article define the crucial points of the operation. please try the error remapping too, not just summing it onto the map. I really think that’ll converge quicker.

you can also get inspiration from this, which inverts a map: https://stackoverflow.com/questions/41703210/inverting-a-real-valued-index-grid

[swanprince]

Thank you for the guidance.

@crackwitz

prepare a target pattern (digital original)

• it should cover the entire view and be decently dense.
• yours looks dense enough, but it doesn’t yet cover the whole view.

Just to confirm your meaning, “target pattern” is a “reference” pattern, correct? In other words, what I want the distorted pattern to eventually look like?

I can also use a more complicated pattern if that would work better for the mapping.

[crackwitz]

@swanprince

Just to confirm your meaning, “target pattern” is a “reference” pattern, correct? In other words, what I want the distorted pattern to eventually look like?

right.

@swanprince

I can also use a more complicated pattern if that would work better for the mapping.

doesn’t have to be complicated. structure/noise across multiple scales will help the optical flow to not be matching the wrong things just because they look similar close-up. that multi-scale structure need not be in a single view. a series of progressively finer grids could be used instead of a single complex pattern.

start with a simple grid. if that goes wrong, you’ll easily see and be able to address it.

the pattern may and should extend beyond the view, so that it covers the view. if this were lens calibration, distortion would be worst in the corners of the view, so that is where having texture would be most important. I don’t know your distortions, so I’ll just assume the same.

“aliasing” of any regular grid/repeating pattern, slipping of gears so to speak, is of no consequence for lens calibration, where the warping is relative to the camera, not relative to the pattern. I don’t quite see where all there is distortion in your setup. your situation might be tolerant/invariant to such aliasing. maybe it requires that no such aliasing occurs, in which case you’d want to use patterns that don’t repeat.

[swanprince]

Just got around to trying out this solution.

@crackwitz

by remapping the map, using the error map. that should converge quickest.

Just to clarify, does this mean instead of doing this:

totalmap += flow

You’d do:

totalmap = cv.remap(src=totalmap, map1=flow, map2=None, interpolation=cv.INTER_CUBIC)

Also, just to make sure, you should not replace imwarped in the first remap call with out on subsequent loops?

Here’s the warped image I’m using, for reference. This is the closest I can place the camera to the surface due to application constraints.

[swanprince]

And here’s the “reference” image:

I can find all the grid intersection points correctly, but using these points in findHomography doesn’t seem to create a very good homography matrix to use in perspectiveTransform; the first temporary output is a gray screen!

Thanks again for your help.

[crackwitz]

I’ve got a headache at the moment, so neocortex not available.

if you’re lucky, you can skip the findHomography and just init with a 3x3 identity matrix.

@swanprince

You’d do:

totalmap = cv.remap(src=totalmap, map1=flow, map2=None, interpolation=cv.INTER_CUBIC)

something of that nature, but I don’t have the concentration to be sure the arguments are what they should be.

@swanprince

Also, just to make sure, you should not replace imwarped in the first remap call with out on subsequent loops?

again same disclaimer. the idea is to always work from the givens and refine the map. no actual image content should ever be warped more than once (im → warp → warp…). that would degrade the content with every iteration. only the map should change from iteration to iteration, from updates that are derived from some error.

I’ll give your two pictures a go when I have the chance.

[crackwitz]

I’m giving this a look now, and because I’m too lazy to find my old code, I’m rediscovering fine points such as using the optflow in reverse because it’s got push/scatter semantics which are contrary to how remap() works.

and I’ll definitely have to inject some estimate of the lighting variations of the actual image. in optical flow there is the brightness constancy assumption and if that isn’t met, results suffer.

a trivial prototype application of DIS optical flow shows that it’s misassigning parts of the grid even though the displacement isn’t so bad that this should happen. I suspect the brightness constancy stuff. I’ll have to fiddle with its parameters. maybe it’s not pyramiding up well enough. maybe I’ll have to swap the optflow algorithm, at least for initialization.

[Steve_in_Denver]

@swanprince

I can find all the grid intersection points correctly, but using these points in findHomography doesn’t seem to create a very good homography matrix to use in perspectiveTransform; the first temporary output is a gray screen!

Since your surface is curved the distortions will not be well described by a perspective transform, so you’ll need something different (a homography won’t work).

If the curved surface can be well approximated as a quadric surface, you might want to look into “quadric transfer” research. is I know there was interest in this topic for immersive displays with curved screens in the early 2000s. Ramesh Raskar at MERL did a lot of work on this, and that would be a good place to start.

Think of quadric transfer as the quadric surface (constrained 3D surface) analog to homography (2D surface). There aren’t functions in OpenCV to handle this, so you’d have to be willing to write your own, but maybe worth pursuing if other options don’t pan out.

[swanprince]

in optical flow there is the brightness constancy assumption and if that isn’t met, results suffer.

I can send over a brighter version of the image, but due to the nature of the camera I’m using I can’t always get the actual image brightness to match the reference image brightness in the field

[crackwitz]

it’s not the total brightness. I appreciate the existing image being fully in range, not overexposed.

it’s the uneven brightness that I need to compensate for. that may not actually be a problem but a goal. unless I can get around it and be lazy, a secondary result of the calculation would be a brightness map you can use to compensate and get an evenly illuminated picture out of it.

as I’m thinking about it… if you could just present a flatfield picture (all plain white image to the projector), that’d make this trivial. just make sure the camera’s exposure settings are locked for both pictures.

Flat-field correction

[swanprince]

Here’s the surface with a flat white background. Same exposure settings, post-processing, etc. as the first image:

Just to be totally clear, this surface is a screen, and as it’s relatively modern there may be some local dimming technology that brightens/darkens parts of it depending on the content it’s showing. Could that be an issue here?

[crackwitz]

@swanprince

some local dimming technology that brightens/darkens parts of it depending on the content it’s showing.

that can have an effect. comparing to the white-on-black grid, I can already see that the unevenness differs. it was worth a try.

the brightness is a secondary concern and should not affect distortion all that much.

[crackwitz]

this post has undergone a couple of edits, which are amendments at the bottom

some pieces out of my current notebook. if you want to “iterate”, run the last three cells repeatedly in sequence.

• https://forum.opencv.org/t/camera-calibration-on-a-curved-surface/22774 · GitHub

actual, actual compensated for brightness variation (actual divided by estimate):

estimating brightness via dilation 10 iterations and np.maximum():

visualization of alignment:

first flow calculation: mean 3.571 px, 0.002 .. 9.147 px

application of first flow yields this alignment:

second flow calculation: mean 0.116 px, 0.000 .. 0.433 px

visualization of alignment:

third flow calculation: mean 0.064 px, 0.000 .. 0.267 px

it’s basically jittering around from noise at this point, i.e. it has converged. the first flow calculation got it almost all of the way there. any iteration after that is just polishing.

cv.remap() uses fixed-point arithmetic, 5 fractional bits. that alone limits the precision (and accuracy) of the result. 2**-5 == 0.03125, so that’s one lower bound on the subpixel precision. the previous (incremental) flow field’s average being 2-3x that limit tells me we’re done iterating.

final flow/map: mean 4.002 px, 0.015 .. 10.089 px

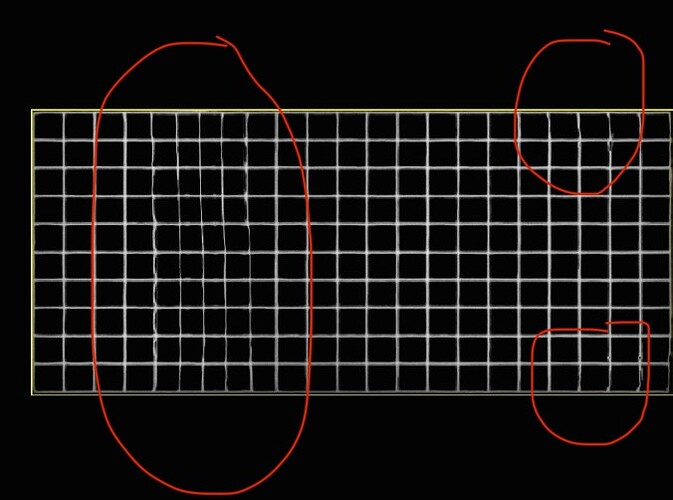
NB: the sliver of “dots” in the top left is actually literally zero. the arrows to the south of it are actually non-zero but small. scale is 1.

and that’s the result:

those bright pixels at the right edge of the difference image come from the way I copy images out of the notebook from VSCode. they are not present in the notebook on github.

the flow/warp field might benefit from lowpassing, as I did a while ago in the other post. wherever the optical flow has no “support”, i.e. no texture/structure to refute any alleged flow, the flow can be whatever. be aware of that. it’s only sensible where the calibration had actual support.

I tried some of the parameters to DIS optical flow. block size had to be increased to at least half the grid spacing, or else it might misassign blocks (“slipping gears”, fencepost problem). optical flow is capable of calculating fine structures. here you’d want it generally smooth, because fine structure would give you strange folds and creases. I’m assuming that the patch size limits the level of detail implicitly, which is to your advantage.

if you need to tease more subpixel precision out of this, the interpolation modes to remap() could be explored. cubic noticeably improved on linear, in terms of the stats I pull out of the flow/warp fields.